Question

Consider the system of linear equations

7x+16y=-2
9x-4y=22
To use the linear combination method and addition to eliminate the y-terms, by which number should the second equation be multiplied?
-4
-1/4
1/4
4

Answer 1

The answer is 4 (for mine 4 was D)

Explanation:

To use the linear combination method and addition to eliminate the y-terms, by which number should the second equation be multiplied?

–4

Negative one-fourth

One-fourth

4

Answer 2

4

Explanation:

The first equation has 16y and the second equation has -4y where both equations are in the same form.

So we need to figure out what we can multiply to -4y such that when added to 16y will give us a sum of 0.

If you don't like that wording, maybe you are more into symbols.

We need to find k such that:

`16y+k(-4y)=0`

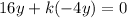
Factor
`y` out:

`(16+k(-4))y=0`

`(16-4k)y=`

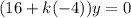
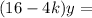
This implies 16-4k=0 since y is a variable and not always 0.

16-4k=0

Subtract 16 on both sides:

-4k=-16

Divide both sides by -4:

k=-16/-4

Simplify:

k=4

So we need to multiply the second equation by 4 so that 16y and -16y will cancel when adding the equations together.

Perhaps you like this wording more:

We need to figure out what the opposite of 16y which is -16y. The reason we wanted to know that is when you add opposites you get 0.

So how do we make -4y be -16y? We need to multiply -4y by 4 which gives you -16y.