Step-by-step explanation:
The given data is as follows.
Initial volume of aspirin = 1.00 L
Initial concentration of aspirin = 0.500 M
Initial pH = 1.86
Hence, hydronium ion concentration will be calculated as follows.
pH =
![-log[H^(+)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/pclsb5d5ztpswphl1czegwokhxu5hzr3m7.png)
or,
![[H^(+)] = 10^(-pH)](https://img.qammunity.org/2020/formulas/chemistry/college/rc0vludijx4qr5z31grr2ij2tcqg7fs15f.png)
=
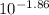
=

As, buffer containing aspirin and its conjugate base is formed in 1 L solution.
Hence, moles of aspirin are 0.500 moles and moles of the conjugate base are 0.25 moles.
So, upon dissociation the concentration of acetylsalicylate ion and hydronium ion are the same.
Hence,
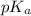 value will be calculated as follows.
value will be calculated as follows.
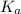 =
=
![([H^(+)]^(2))/([Aspirin])](https://img.qammunity.org/2020/formulas/chemistry/college/80e1rnxhdyg1gphq8jg7t3dj1nrwgfa2gh.png)
=
![([13.8 * 10^(-3)]^(2))/(0.50)](https://img.qammunity.org/2020/formulas/chemistry/college/y1a9tlxlm0v7w2nr0rsuwgqurprcsjvm3t.png)
=
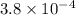
Also,
![pK_(a) = -log [K_(a)]](https://img.qammunity.org/2020/formulas/chemistry/college/in1twut84nnkvpx3kl3drlrdjfw8rp9nqc.png)
=
![-log [3.8 * 10^(-4)]](https://img.qammunity.org/2020/formulas/chemistry/college/506mfxfjxic8n38z0dq097xcpacle53tkn.png)
= 3.41
Now, using Henderson-Hasselbalch equation we determine the pH as follows.
pH =
![pK_(a) + log ([CH_(3)COO^(-)])/([Aspirin])](https://img.qammunity.org/2020/formulas/chemistry/college/gsixf85erfnjzum3ixlc8v2mhwswq7njq7.png)
= 3.41 +
![log ([0.25])/([0.5])](https://img.qammunity.org/2020/formulas/chemistry/college/4u4xhs2aik3ikxgg8769wg9c3kdgcv60ja.png)
= 3.11
Determine the hydronium ion concentration of buffer as follows.
![[H^(+)] = 10^(-pH)](https://img.qammunity.org/2020/formulas/chemistry/college/rc0vludijx4qr5z31grr2ij2tcqg7fs15f.png)
=
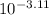
=
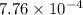 M
M
Therefore, we calculate the recent dissociation as follows.
% dissociation =

=
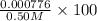
=
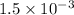 × 100
× 100
= 0.15%
Thus, we can conclude that the value of % dissociation of new buffered solution is 0.15%.