Answer:
1) Even for first problem.
2) Neither for the second.
I really think the problem I labeled 1 is the correct interpretation but just in case you meant the latter I wrote the latter as well. The sentence translates to exactly what I have for problem number 1.
The Problem:
1) Determine if
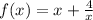 is even, odd, or neither.
is even, odd, or neither.
2) Determine if
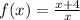 is even, odd, or neither.
is even, odd, or neither.
Explanation:
 implies
implies
 is even.
is even.
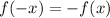 implies
implies
 is odd.
is odd.
So either definition says we have to plug in
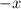 .
.
1)
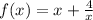 with new input
with new input
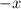 :
:
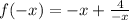
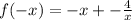
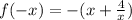
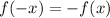
This means
 is even since we got the same thing we started with.
is even since we got the same thing we started with.
2)
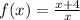 with new input
with new input
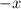 :
:
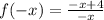
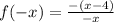
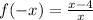
This is neither the same or the opposite of what we started with.