Question

HELPPP!!!!!!!!!!!!!!!! PLEASE! :D

Answer 1

The solution to the inequality is:

`-1\le \:x\le \:3`

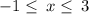
The line graph of the solution is also attached.

Explanation:

Given the expression

`4x-1\:\le \:5x\:\le \:3\left(x+2\right)`

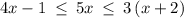
solving the expression

`4x-1\:\le \:5x\:\le \:3\left(x+2\right)`

• 
  `\mathrm{If}\:a\le \:u\le \:b\:\mathrm{then}\:a\le \:u\quad \mathrm{and}\quad \:u\le \:b`

`4x-1\le \:5x\quad \mathrm{and}\quad \:5x\le \:3\left(x+2\right)`

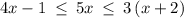
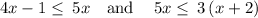
solving

`4x-1\le \:5x`

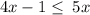
Add 1 to both sides

`4x-1+1\le \:5x+1`

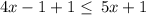
Simplify

`4x\le \:5x+1`

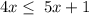
Subtract 5x from both sides

`4x-5x\le \:5x+1-5x`

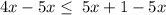
simplify

`-x\le \:1`

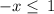
Multiply both sides by -1 (reverse inequality)

`\left(-x\right)\left(-1\right)\ge \:1\cdot \left(-1\right)`

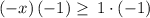
Simplify

`x\ge \:-1`

Similarly solving

`5x\le \:3\left(x+2\right)`

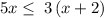
Subtract 3x from both sides

`5x-3x\le \:3x+6-3x`

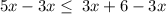
Simplify

`2x\le \:6`

Divide both sides by 2

`(2x)/(2)\le (6)/(2)`

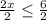
Simplify

`x\le \:3`

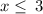
So combine the interval

`x\ge \:-1\quad \mathrm{and}\quad \:x\le \:3`

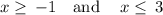
Merge overlapping intervals

`-1\le \:x\le \:3`

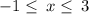
Therefore, the solution to the inequality is:

`-1\le \:x\le \:3`

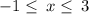
The line graph of the solution is also attached.