Answer:
D. The star is approaching Earth.
Step-by-step explanation:
As we know by the doppler's effect of light that

here we know that
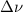 = change in frequency
= change in frequency
here we know that the wavelength of light coming from the star is decreased so the frequency will increase

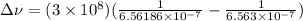
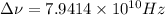
now we have
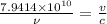
here we know that

now we have
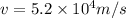
So here correct answer is
D. The star is approaching Earth.