Answer:
Velocity = 4.41×10⁵ m/s
Step-by-step explanation:
The force of attraction between the nucleus and the electron is equal to the centrifugal force acting on the outermost electron due to circular rotation. It can be mathematically written as:
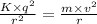
Where,
K is the Coulomb's constant having value 9×10⁹ N. m²/C²
q is the charge on the electron or the proton which is 1.6×10⁻¹⁹ C
r is the radius of the atom
m is the mass of the electron having value 9.1×10⁻³¹ Kg
v is the velocity of the electron.
The equation can be written to calculate the velocity as:

Given that:
r = 1.3×10⁻⁹ m
So,

Velocity = 4.41×10⁵ m/s