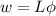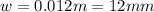Question

Red light of wavelength 633 nm from a helium-neon laser passes through a slit 0.380 mm wide. The diffraction pattern is observed on a screen 3.55 m away. Define the width of a bright fringe as the distance between the minima on either side.

Answer 1

width of maximum intensity at the center of screen is 12 mm

Step-by-step explanation:

Position of minimum intensity on the screen is given as

`a sin\theta = N\lambda`

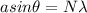
now we know that for first position of minimum intensity on the screen we have

`N = 1`

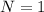
now we know

`a sin\theta = 1 \lambda`

`a = 0.380 mm`

`\lambda = 633 nm`

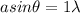
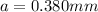
now we have

`(0.380 * 10^(-3))sin\theta = (633 * 10^(-9))`

`\theta = 0.095  degree = 1.66 * 10^(-3) rad`

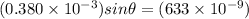
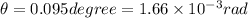
now total angular width of central maximum is given as

`\phi = 2\theta = 2(1.66 * 10^(-3)) rad`

`\phi = 3.33 * 10^(-3) rad`

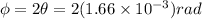
now linear width is given as

`w = L\phi`

`w = (3.55)(3.33 * 10^(-3))`

`w = 0.012 m = 12 mm`