Question

Himpunan penyelesaian pertidaksamaan nilai mutlak |2x-4| > |3x+2|

Answer 1

The solution in interval notation is:

`(-6,(2)/(5))`.

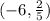The solution in inequality notation is:

`-6<x<(2)/(5)`.

Explanation:

I think you are asking how to solve this for
`x`.

Keep in mind
`|x|=√(x^2)`.

`|2x-4|>|3x+2|`

`√((2x-4)^2)>√((3x+2)^2)`

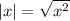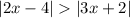
If
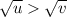`√(u)>√(v)` then
`u>v`.

`(2x-4)^2>(3x+2)^2`

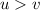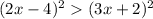
Subtract
`(2x-4)^2` on both sides:

`0>(3x+2)^2-(2x-4)^2`

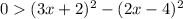
Factor the difference of squares
`a^2-b^2=(a-b)(a+b)`:

`0>((3x+2)-(2x-4))((3x+2)+(2x-4))`

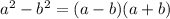Simplify inside the factors:

`0>(x+6)(5x-2)`

`(x+6)(5x-2)<0`

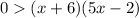
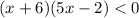
The left hand side is a parabola that faces up. I know this because the degree is 2.

The zeros of the the parabola are at x=-6 and x=2/5.

We can solve x+6=0 and 5x-2=0 to reach that conclusion.

x+6=0

Subtract 6 on both sides:

x=-6

5x-2=0

Add 2 on both sides:

5x=2

Divide both sides by 5:

x=2/5

Since the parabola faces us and
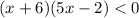`(x+6)(5x-2)<0` then we are looking at the interval from x=-6 to x=2/5 as our solution. That part is where the parabola is below the x-axis. We are looking for where it is below since it says the where is the parabola<0.

The solution in interval notation is:

`(-6,(2)/(5))`.

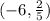The solution in inequality notation is:

`-6<x<(2)/(5)`.