Answer: 653.011Mpc
Step-by-step explanation:
Hubble deduced that the farther the galaxy is, the more redshifted it is in its spectrum, and noted that all galaxies are "moving away from each other with a speed that increases with distance", and enunciated the now called Hubble–Lemaître Law.
This is mathematically expressed as:
 (1)
(1)
Where:
 is the approximate recession velocity of the galaxy
is the approximate recession velocity of the galaxy
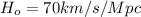 is the current Hubble constant
is the current Hubble constant
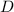 is the galaxy's distance
is the galaxy's distance
On the other hand, the equation for the Doppler shift is:
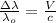 (2)
(2)
Where:
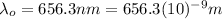 is the wavelength for the Ha line of the galaxy observed at rest
is the wavelength for the Ha line of the galaxy observed at rest
 is the variation between the measured wavelength for the Ha emission line in the spectrum of this galaxy (
is the variation between the measured wavelength for the Ha emission line in the spectrum of this galaxy (
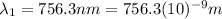 in this case) and the wavelength for the same Ha line observed at rest
in this case) and the wavelength for the same Ha line observed at rest
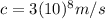 is the speed of light
is the speed of light
Rewriting (2):
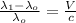 (3)
(3)
Isolating
 :
:
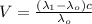 (4)
(4)
Finding
 :
:
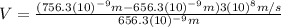 (5)
(5)
 (6)
(6)
Substituting
 in (1):
in (1):
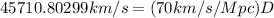 (7)
(7)
Finding
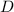 :
:
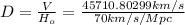 (8)
(8)
Finally:
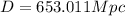 (8) This is the galaxy's distance
(8) This is the galaxy's distance