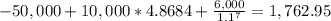Question

If Quail Company invests $50,000 today, it can expect to receive $10,000 at the end of each year for the next seven years, plus an extra $6,000 at the end of the seventh year. (PV of $1, FV of $1, PVA of $1, and FVA of $1) (Use appropriate factor(s) from the tables provided. Round your present value factor to 4 decimals.) What is the net present value of this investment assuming a required 10% return on investments?

Answer 1

Net Present Value = $1,762.95

Step-by-step explanation:

Equal payments made at the end of each year implies that the cash inflows from year 1 to 7 form an annuity where:

`PVof An Ordinary Annuity= (PMT[1-(1+i)^(-n) ] )/(i)`

where PMT is the the equal payment cash inflow received at the end of each period and

`([1-(1+i)^(-n) ] )/(i)` = The present value of an annuity factor for n years at i%

The present value of an annuity factor for 7 years at 10% equals

`([1-(1+0.1)^(-7) ] )/(0.1)=4.8684`

therefore: Net Present value of this investment given a 10% return o investments equals

`-50,000+10,000*4.8684+(6,000)/(1.1^7)=1,762.95`