Question

Scientist can determine the age of ancient objects by a method called radiocarbon dating. The bombardment of the upper atmosphere by cosmic rays converts nitrogen to a radioactive isotope of carbon, 14C, with a half-life of about 5730 years. Vegetation absorbs carbon dioxide through the atmosphere and animal life assimilates 14C through food chains. When a plant or animal dies, it stops replacing its carbon and the amount of 14C begins to decrease through radioactive decay. Therefore, the level of radioactivity must also decay exponentially. A parchment fragment was discovered that had about 64% as much 14C radioactivity as does plant material on Earth today. Estimate the age of the parchment. (Round your answer to the nearest hundred years.) yr

Answer 1

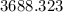`3688.323`years

Step-by-step explanation:

Given-

Half life of
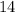`14`C
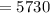`= 5730`years

As we know -

`A_((t)) = A_0e^(kt)`

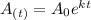
Where

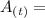`A_((t)) =` Mass of radioactive carbon after a time period "t"

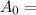`A_0=` initial mass of radioactive carbon

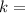`k =`radioactive decay constant

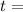`t =`time

First we will find the value of "k"

`(1)/(2) = (1)*e^(k*5730)\\`

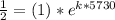
On solving, we get -

`e^(5730*k)= 0.5\\5730*k = ln(0.5)\\k = -0.000121`

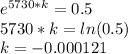
Now, when mass of 14C becomes
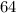`64`% of the plant material on earth today, then its age would be

`A_((t)) = A_0*e^((-0.000121*t))\\A_((t))= 0.64*A_0\\0.64*A_0 = A_0*e-^((0.000121*t))\\t = 3688.323`years