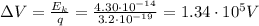Question

An alpha particle (q = +2e, m = 4.00 u) travels in a circular path of radius 6.40 cm in a uniform magnetic field with B = 1.17 T. Calculate (a) its speed, (b) its period of revolution, (c) its kinetic energy, and (d) the potential difference through which it would have to be accelerated to achieve this energy.

Answer 1

Step-by-step explanation:

It is given that,

Charge on alpha, q = 2e

Radius of circular path, r = 6.4 cm = 0.064 m

Mass of alpha particle, m = 4 u

Uniform magnetic field, B = 1.17 T

(a) Magnetic force is balanced by the centripetal force as :

`qvB=(mv^2)/(r)`

`v=(qrB)/(m)`

`v=(2* 1.6* 10^(-19)* 0.064* 1.17 )/(6.64* 10^(-27))`

`v=3.6* 10^6\ m/s`

(b) Period of revolution,
`T=(2\pi r)/(v)`

`T=(2\pi 0.064 )/(3.6* 10^6)`

`T=1.11* 10^(-7)\ s`

(c) Kinetic energy,
`E=(1)/(2)mv^2`

`E=(1)/(2)* 6.64* 10^(-27)* (3.6* 10^6)^2`

`E=4.3* 10^(-14)\ J`

or

`E=268750\ eV`

(d) Potential energy = Kinetic energy

`2eV=E`

`2eV=268750\ eV`

V = 134375 volts

Hence, this is the required solution.

Answer 2

(a)
`3.59\cdot 10^6 m/s`

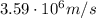
The magnetic force acts as centripetal force, so we can write

`qvB= (mv^2)/(r)`

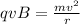
where

q is the charge of the particle

v is its speed

B is the magnetic field strength

m is the mass

r is the radius of the circular path

For the alpha particle in the problem,

`q=2e=3.2\cdot 10^(-19) C`

`m=4.00 u = 4\cdot 1.67\cdot 10^(-27) kg=6.68\cdot 10^(-27) kg`

`r = 6.40 cm = 0.064 m`

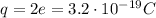
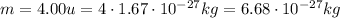
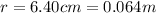
B = 1.17 T

Re-arranging the equation and solving for v, we find its speed:

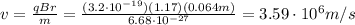
`v=(qBr)/(m)=((3.2\cdot 10^(-19))(1.17)(0.064 m))/(6.68\cdot 10^(-27))=3.59\cdot 10^6 m/s`

(b)
`1.12\cdt 10^(-7) s`

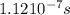
The period of revolution is given by the ratio between the distance travelled in one circle (so, the circumference of the path) and the speed of the particle, so

`T= (2\pi r)/(v)`

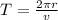
where

r is the radius of the path

v is the speed

Here we have

`r = 6.40 cm = 0.064 m`

`v=3.59\cdot 10^6 m/s`

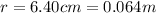
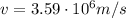
So the period of revolution is

`T= (2\pi (0.064))/(3.59\cdot 10^6)=1.12\cdt 10^(-7) s`

(c)
`4.30\cdot 10^(-14)J`

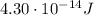
The kinetic energy of a particle is given by

`E_k = (1)/(2)mv^2`

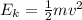
where

m is its mass

v is its speed

For the alpha particle in the problem, we have

`m=4.00 u = 4\cdot 1.67\cdot 10^(-27) kg=6.68\cdot 10^(-27) kg`

`v=3.59\cdot 10^6 m/s`

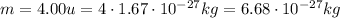
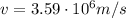
So its kinetic energy is

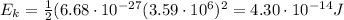
`E_k = (1)/(2)(6.68\cdot 10^(-27)(3.59\cdot 10^6)^2=4.30\cdot 10^(-14)J`

(d)
`1.34\cdot 10^5 V`

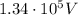
When accelerated through a potential difference, a particle gains a kinetic energy equal to the change in electric potential energy - so we can write:

`q \Delta V = E_k`

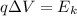
where the term on the left is the change in electric potential energy, with

q is the charge of the particle

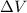`\Delta V` is the potential difference

Here we have

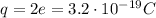`q=2e=3.2\cdot 10^(-19) C` is the charge of the alpha particle

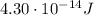`4.30\cdot 10^(-14)J` is the kinetic energy

Re-arranging the formula, we find

`\Delta V=(E_k)/(q)=(4.30\cdot 10^(-14))/(3.2\cdot 10^(-19))=1.34\cdot 10^5 V`