Answer:
The tangent line to the given curve at the given point is
 .
.
Explanation:
To find the slope of the tangent line we to compute the derivative of
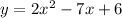 and then evaluate it for
and then evaluate it for
 .
.
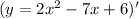 Differentiate the equation.
Differentiate the equation.
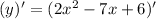 Differentiate both sides.
Differentiate both sides.
 Sum/Difference rule applied:
Sum/Difference rule applied:

 Constant multiple rule applied:
Constant multiple rule applied:
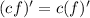
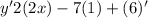 Applied power rule:
Applied power rule:
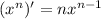
 Simplifying and apply constant rule:
Simplifying and apply constant rule:
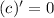
 Simplify.
Simplify.
Evaluate y' for x=4:
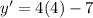
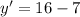
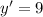 is the slope of the tangent line.
is the slope of the tangent line.
Point slope form of a line is:

where
 is the slope and
is the slope and
 is a point on the line.
is a point on the line.
Insert 9 for
 and (4,10) for
and (4,10) for
 :
:

The intended form is
 which means we are going need to distribute and solve for
which means we are going need to distribute and solve for
 .
.
Distribute:
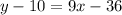
Add 10 on both sides:

The tangent line to the given curve at the given point is
 .
.
------------Formal Definition of Derivative----------------
The following limit will give us the derivative of the function
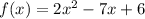 at
at
 (the slope of the tangent line at
(the slope of the tangent line at
 ):
):
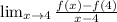
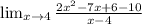 We are given f(4)=10.
We are given f(4)=10.
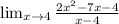
Let's see if we can factor the top so we can cancel a pair of common factors from top and bottom to get rid of the x-4 on bottom:
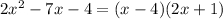
Let's check this with FOIL:
First:
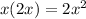
Outer:
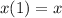
Inner:
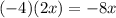
Last:
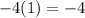
---------------------------------Add!
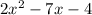
So the numerator and the denominator do contain a common factor.
This means we have this so far in the simplifying of the above limit:
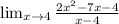

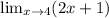
Now we get to replace x with 4 since we have no division by 0 to worry about:
2(4)+1=8+1=9.