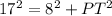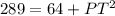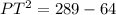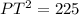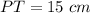Question

If PT is a tangent at Y to a circle whose centre is O and OP is 17cm ,It is 8cm find the length of the tangent segment PT

Answer 1

`PT=15\ cm`

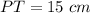
Explanation:

we know that

PT is tangent at T to a circle whose center is O

That means----> Segment PT and segment OT are perpendicular lines

so

Triangle OPT is a right triangle

see the attached figure to better understand the problem

In the right triangle OPT of the figure

Applying the Pythagoras Theorem

`OP^(2)=OT^(2)+PT^(2)`

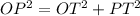
we have

`OP=17\ cm`

`OT=8\ cm`

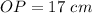
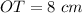
substitute and solve for PT

`17^(2)=8^(2)+PT^(2)`

`289=64+PT^(2)`

`PT^(2)=289-64`

`PT^(2)=225`

`PT=15\ cm`