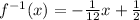Answer:
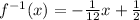
Explanation:
* Lets explain how to find the inverse function
- If f(x) = y, then its inverse is
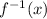
- To find the inverse function we switch x and y and solve to find the
new y
- The domain of the function f(x) = y is x and its range is y
- The domain of
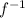 is y and its range is x
is y and its range is x
* Lets solve the problem
∵ f(x) = -12x + 6
∵ f(x) = y
∴ y = -12x + 6
- Lets switch x and y to find the inverse of f(x)
∵ y = -12x + 6
∴ x = -12y + 6
- Lets solve for y
∵ x = -12y + 6
- Subtract 6 from both sides
∴ x - 6 = -12y
- Divide both sides by -12
∴
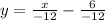
- Remember x/-12 is the same as (-1/12)x and (-)(-) = (+)
∴
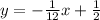
∴