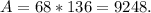Question

"A developer wants to enclose a rectangular grassy lot that borders a city street for parking. If the developer has 272 feet of fencing and does not fence in the side along the street, what is the largest area that can be enclosed?"

Answer 1

The largest area that can be enclosed is 9248 square feet.

Explanation:

This is a typical problem of optimization that can be solved using derivatives. We have a rectangular region, and let us denote the height by
`x`, and the base by
`y`.

Then, the area of the rectangle is
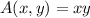`A(x,y)=xy`. Notice that the area is a function of
`x` and
`y`, but if we want to use calculus, we should have only one variable. This can be done if we find a relationship between both variables.

Recall that the fences will not bu used in the whole perimeter of the rectangular area, but only in three sides. Hence,
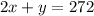`2x+y=272`. (Without lost of generality we can consider
`2y+x=272`, instead.)

Then,
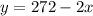`y=272-2x` ans substituting in the formula for the area:

`A(x) = x(272-2x) = 272x-2x^2.`

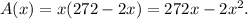
Taking derivative with respect to x:

`A'(x) = 272-4x.`

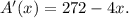
Its only zero can be found solving the equation
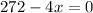`272-4x=0`. Hence, its only zero of
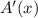`A'(x)` is
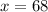`x=68`. In order to assure that 68 is a point of maximum, we find
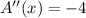`A''(x) = -4` and conclude that, in effect, 68 is a point of maximum.

We obtain the value of
`y` substituting the value of
`x` in the relationship between both variables:
`y=272-2*68=136`. With the values of
`x` and
`y` we can calculate the desired area:

`A=68*136=9248.`