Answer:
The energy and the wavelength of the photon are 1.546 MeV and
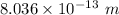 .
.
Step-by-step explanation:
Given that,
Kinetic energy = 261 KeV
Planck's constant
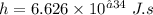
Speed of light
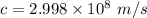
Mass of electron
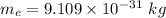
Charge
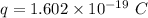
(A). We need to calculate the energy of the photon
Using formula of rest mass energy
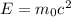
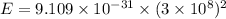
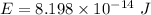
Energy in eV
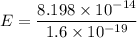
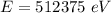
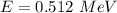
The total energy of photon
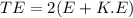
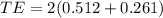
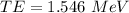
(B). We need to calculate the wavelength of the photon
Using formula of wavelength
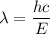
Put the value into the formula
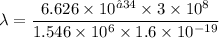
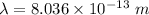
Hence, The energy and the wavelength of the photon are 1.546 MeV and
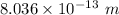 .
.