Question

You measure the weight of 49 backpacks, and find they have a mean weight of 67 ounces. Assume the population standard deviation is 8.8 ounces?. Based on this, what is the maximal margin of error associated with a 94% confidence interval for the true population mean backpack weight.

Answer 1

Answer: 2.36

Explanation:

The formula to find the margin of error is given by :-

`E=z_(\alpha/2)(\sigma)/(√(n))`

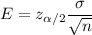
Given : Significance level :
`\alpha: 1-0.94=0.06`

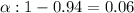
Critical value :
`z_(\alpha/2)=1.88` [Using standard normal distribution table]

Sample size : n=49

Standard deviation : 8.8 ounces

Then , the margin of error will be :-

`E=(1.88)(8.8)/(√(49))\\\\\Rightarrow\ E=2.36342857143\approx2.36`

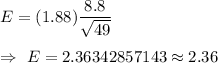
Hence, the margin of error associated with a 94% confidence interval for the true population mean backpack weight = 2.36