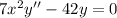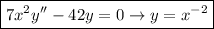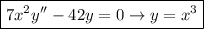Answer:
a)
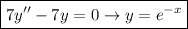 .
.
b)
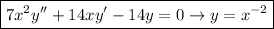
c)
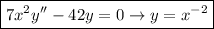
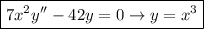
Explanation:
a) The given differential equation is:
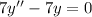 .
.
The characteristic equation is:

This implies that:
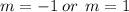
The auxiliary solution to this second order homogeneous differential equation is:
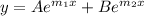
Therefore any equation of the
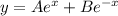 where A and B are constants is a solution
where A and B are constants is a solution
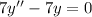 .
.
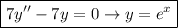 .
.
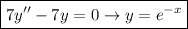 .
.
b) The given differential equation is:

The characteristic equation is given by:
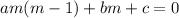 , where a=7, b=14 and c=-14
, where a=7, b=14 and c=-14
This implies that:
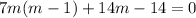

The auxiliary equation is of the form:
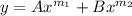 where A and B are constants.
where A and B are constants.
Hence any equation of the form:
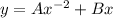 is a solution to
is a solution to

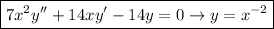
c) The given differential equation is:
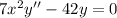
The characteristic equation is given by:
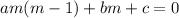 , where a=7, b=0 and c=-42
, where a=7, b=0 and c=-42
This implies that:
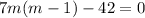
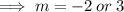
The auxiliary equation is of the form:
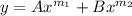 where A and B are constants.
where A and B are constants.
Hence any equation of the form:
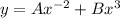 is a solution to
is a solution to