Answer:
The energy delivered to the circuit during one period is 177.87 mJ.
Step-by-step explanation:
Given that,
Resistance
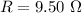
Inductance L=8.50 mH
Capacitance
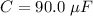
Voltage
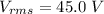
We need to calculate the resonance frequency
Using formula of resonance frequency
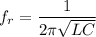
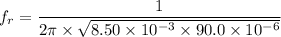
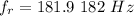
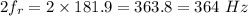
We need to calculate the period
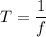
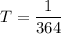
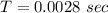
We need to calculate the inductive resistance
Using formula of inductive resistance


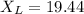
We need to calculate the capacitive resistance
Using formula of capacitive resistance
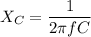
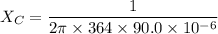

We need to calculate the impedance
Using formula of impedance
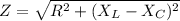
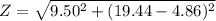

We need to calculate the angle
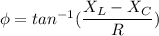

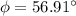
We need to calculate the energy
Using formula of energy
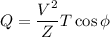
Put the value into the formula
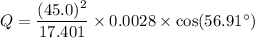
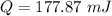
Hence, The energy delivered to the circuit during one period is 177.87 mJ.