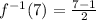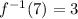Answer:
a)
 , b)
, b)
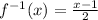 , c)
, c)
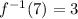
Explanation:
a) We evaluate the function at
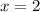 :
:
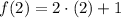
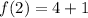

b) First, we determine the inverse of the function by algebraic means:
1)
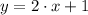 Given
Given
2)
![y +(-1) = 2\cdot x + [1+(-1)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/yrda1upmx6skb0bbgzrxskp90373bsukmz.png) Compatibility with addition/Associative property
Compatibility with addition/Associative property
3)
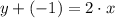 Existence of additive inverse/Modulative property
Existence of additive inverse/Modulative property
4)
![2^(-1)\cdot [y+(-1)] = (2\cdot 2^(-1))\cdot x](https://img.qammunity.org/2022/formulas/mathematics/high-school/vc1nww1xxhi9tki8anv13eqexr2bu1l7ho.png) Compatibility with multiplication/Commutative and associative properties
Compatibility with multiplication/Commutative and associative properties
5)
![[y+(-1)]\cdot 2^(-1) = x](https://img.qammunity.org/2022/formulas/mathematics/high-school/s56xfkhvsurhczjxop2kygbfwoivds0nfw.png) Existence of multiplicative inverse/Modulative and commutative properties
Existence of multiplicative inverse/Modulative and commutative properties
6)
![x = [y+(-1)]\cdot 2^(-1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/aqds4e1rcg8kdwqif0f6hwshzs4krfpow9.png) Symmetry property of equality
Symmetry property of equality
7)
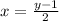 Definitions of subtraction and division
Definitions of subtraction and division
8)
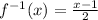
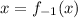 /
/
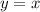 /Result
/Result
c) Now we evaluate the expression obtained on b) at the given number: