Answer:
The speed of the electron and the radius of the circular path are
 and
and
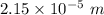 .
.
Step-by-step explanation:
Given that,
Magnetic field = 0.275 T
Kinetic energy
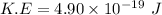
We need to calculate the speed of the electron
Using kinetic energy

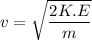
Where, m = mass of electron
K.E = kinetic energy
Put the value into the formula
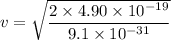
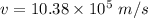
We need to calculate the radius of the circular path
Using equation of force on charge in magnetic field
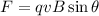 ....(I)
....(I)
Using centripetal force
 ....(II)
....(II)
From equation (I) and (II)
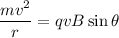
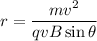
Put the value into the formula
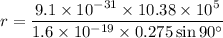
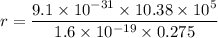
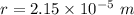
Hence, The speed of the electron and the radius of the circular path are
 and
and
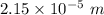 .
.