Answer: The given series neither converges nor diverges.
Step-by-step explanation: We are given to determine whether the following series converges or diverges :
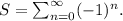
If the series converges, we are to find its sum.
The given series can be written as :
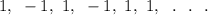
We note that the given series is a geometric one with first term 1 and common ratio given by
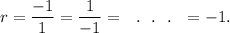
We know that a geometric series with common ratio r converges if |r| <1 and diverges if |r| > 1.
Since |r| = 1 for the given series, so the series will neither converge nor diverge.
Thus, the given series neither converges nor diverges.