Answers: G) ∠BCS = 57.5°
H) ∠FHI = 72°
I) ∠ACB and also ∠DCH
J) ∠CHD (which can also be named ∠BHE)
Explanation:
First of all, I checked your answers for A-F and they are all correct. YAY!
********************************************************************************************
G) Draw a point halfway between B and D and label it S. Then draw a ray from C passing through S.
∠ACB and ∠BCD are supplementary so
65° + ∠BCD = 180°
⇒ ∠BCD = 115°
Since ray CS bisects ∠BCD, then ∠BCS is half of ∠BCD.
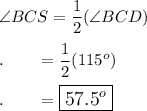
********************************************************************************************
H) The instructions state to draw a line from H to F. This divides ∠DHI into two angles: ∠FHD and ∠FHI. Since lines BI and EG are perpendicular, then ∠DHI = 90°. It is given that ∠FHI is 4 times larger than ∠FHD so we can use substitution...
∠FHD + ∠FHI = ∠DHI
∠FHD + 4(∠FHD) = 90°
5(∠FHD) = 90°
∠FHD = 18°
∠FHI = 4(∠FHD)
= 4 (18°)
=
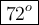
********************************************************************************************
I) adjacent means they share a side and supplementary means they form a straight angle. There are two angles that are adjacent and supplementary to ∠ACH.
- ACB - they share side AC and are supplementary on BH
- DCH - they share side CH and are supplementary on AD
********************************************************************************************
J) congruent means equal and adjacent means they share a side.
The angle that is not congruent nor adjacent to ∠GHI is its vertical angle, which is ∠CHD. Notice that ∠CHD is the same as ∠BHE.