For this case we have to find the area through Heron's formula:
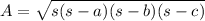
Where:
s: It's half the perimeter of the triangle
a, b, c are the sides.
We can find the sides by equating the distance between two points:
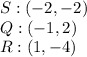
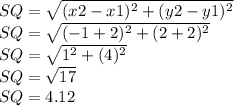
We found QR:
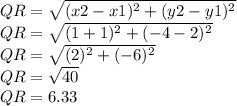
We found RS:
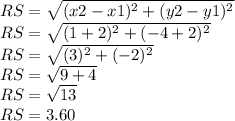
So, half of the perimeter is:
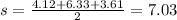
Thus, the area is:

Rounding we have that the area is 7 square units
Answer:
Option A