Question

What is the area of triangle QRS?

7 square units

9 square units

10 square units

13 square units



the answer is 7 square units

Answer 1

If you are looking for an explanation..

Explanation:

It is 7 because if you use the box it out method, you would get 4 triangles and 1 primary one to look for. the other 3 would be 3,2, and 6. Added it would be 11 and subtracted from the rectangles, 18 you would get 7.

Answer 2

For this case we have to find the area through Heron's formula:

`A = √(s (s-a) (s-b) (s-c))`

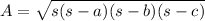
Where:

s: It's half the perimeter of the triangle

a, b, c are the sides.

We can find the sides by equating the distance between two points:

`S: (- 2, -2)\\Q: (- 1,2)\\R: (1, -4)`

`SQ=\sqrt {(x2-x1) ^ 2+(y2-y1) ^ 2}\\SQ=\sqrt {(- 1 + 2) ^ 2+ (2 + 2) ^ 2}\\SQ=\sqrt {1 ^ 2 +(4) ^2}\\SQ=\sqrt {17}\\SQ=4.12`

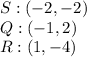
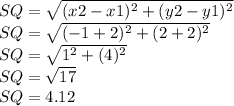
We found QR:

`QR = \sqrt {(x2-x1) ^ 2 + (y2-y1) ^ 2}\\QR = \sqrt {(1 + 1) ^ 2 + (- 4-2) ^ 2}\\QR = \sqrt {(2) ^ 2 + (- 6) ^ 2}\\QR = \sqrt {40}\\QR = 6.33`

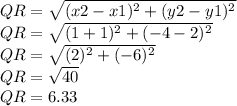
We found RS:

`RS=√((x2-x1)^2+(y2-y1)^2)\\RS=√((1 + 2)^2+(- 4 + 2)^2)\\RS=√((3)^2+(- 2)^2)\\RS=√(9+4)\\RS=\sqrt {13}\\RS=3.60`

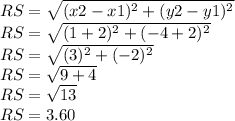
So, half of the perimeter is:

`s = \frac {4.12 + 6.33 + 3.61} {2} = 7.03`

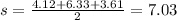
Thus, the area is:

`A = √(7.03 (7.03-4.12) (7.03-6.33) (7.03-3.61))\\A = √(7.03 (2.91) (0.7) (3.42))\\A = \sqrt {48.97}\\A = 6,997`

Rounding we have that the area is 7 square units

Answer:

Option A