Answer:
1,313,400 winning combinations of people are possible
Explanation:
Total number of tickets sold = 200
This means there are total 200 possible options for the winning tickets and only 3 winners will be selected. So we have to select 3 winners out of 200. It is stated that the order of selection doesn't matter, this means this is a problem of combinations.
Winning combinations of 3 people out of 200 means, we have to find the number of combinations of 200 people taken 3 at a time which can be represented as 200C3.
The formula for combinations is:
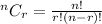
So, for the given case it would be:
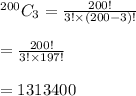
This means, 1,313,400 winning combinations of people are possible.