Question

Determine the eccentricity of the ellipse given by 9x^2+16y^2-72x+64y-368=0

Answer 1

`e=0.66`

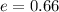
Explanation:

The eccentricity of an ellipse is given by:
`e=\sqrt{1-(b^2)/(a^2) }`

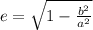
The given ellipse has equation:
`9x^2+16y^2-72x+64y-368=0`

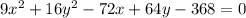
We can rewrite this equation in standard form to obtain:

`((x-4)^2)/(8^2)+(y+2)/(6^2)=1`

We compare to the general standard form equation:
`((x-h)^2)/(a^2)+(y-k)/(b^2)=1`

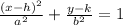
to get:
`a=8,b=6`

We substitute into the eccentricity formula to get:

`e=\sqrt{1-(6^2)/(8^2) }`

`e=(√(7))/(4)=0.661438`

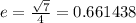
The eccentricity is 0.66 to the nearest hundredth