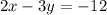Answer:

Explanation:
The point-slope form of an equation of a line:
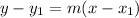
m - slope
The formula of a slope:
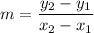
=============================================
We have two points (-6, -2) and (6, 8).
Calculate the slope:
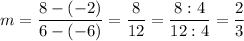
Put it and the coordinates of the point (6, 8) to the equation of a line:
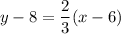
Convert to the slope-intercept form y = mx + b:
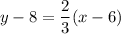 use the distributive property a(b + c) = ab + ac
use the distributive property a(b + c) = ab + ac
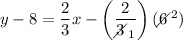
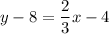 add 8 to both sides
add 8 to both sides
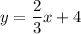
Convert to the standard form Ax + By = C:
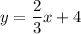 multiply both sides by 3
multiply both sides by 3
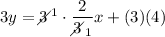
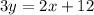 subtract 2x from both sides
subtract 2x from both sides
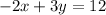 change the signs
change the signs