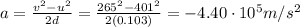Question

An indestructible bullet 2.27 cm long is fired

straight through a board that is 8 cm thick.
The bullet strikes the board with a speed of
401 m/s and emerges with a speed of 265 m/s.
What is the average acceleration of the bullet through the board?
Answer in units of m/s
2

Answer 1

`-4.40\cdot 10^(5) m/s^2`

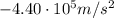
Step-by-step explanation:

We can assume that the bullet decelerates only when it is passing through the board, from the moment it starts touching the board until it leaves it completely; so, it accelerates for a total distance of

d = 2.27 cm + 8 cm = 10.27 cm = 0.103 m

So we can use the following equation to find its acceleration:

`v^2 - u^2 = 2ad`

where

v = 265 m/s is the final speed of the bullet

u = 401 m/s is its initial speed

a is the acceleration

d = 0.103 m

Solving for a,

`a=(v^2-u^2)/(2d)=(265^2-401^2)/(2(0.103))=-4.40\cdot 10^(5) m/s^2`