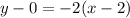Answer:
Parallel:
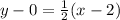
Perpendicular:
Explanation:
Parallel lines have the same slope.
Perpendicular lines have opposite reciprocal slopes.
The point slope form of a line is:

where
 is a point on the line and
is a point on the line and
 is the slope.
is the slope.
To find the slope we will first have to find the slope of the given line.
We are going to put it into slope-intercept form
 because it tells us the slope,m, which is what we need.
because it tells us the slope,m, which is what we need.
Parallel lines will have the same slope,
 .
.
Perpendicular lines will have the opposite reciprocal slope:
 .
.
So let's put
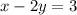 into
into
 form by solving for
form by solving for
 .
.
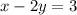
Subtract
 on both sides:
on both sides:
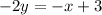
Divide both sides by -2:

Simplify:

or
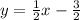 .
.
So the slope is 1/2 for the given equation.
Our parallel line will also have slope 1/2.
Our perpendicular line will have slope -2.
Let's move onto finding these equations starting with the parallel one.

Plug in
 and
and
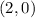 :
:
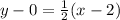
Now the perpendicular one:

Plug in
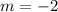 and
and
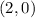 :
: