Answer:
None of these.
Please make sure you have written the choices correctly and check the question please.
The problem and choices I see:
Which complex number has a distance of 17 from the origin on the complex plane?
A) 2+15i
B) 17+i
C)20-3i
D)4-i
Explanation:
A complex number,
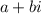 , and the point
, and the point
 has distance:
has distance:
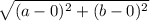 by distance formula.
by distance formula.
Simplifying this gives us:
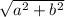
So we are looking for
 in your choices so that
in your choices so that
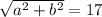 .
.
Let's begin.
Choice 1:
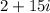
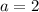
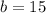
So
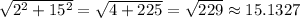 .
.
So choice A is out if I interpreted it correctly.
Choice 2:

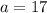
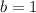
So
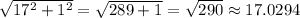 .
.
So choice B is out.
Choice 3:


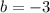
So
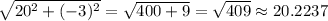
So choice C is out.
Choice 4:
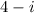
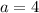
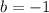
So
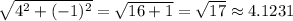
So choice D is out.
So it would be none of these have a distance of 17 from the origin.