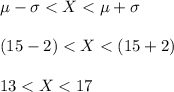Answer: First Option
Approximately 13–17 pounds
Explanation:
We know that the mean weight of dogs is:
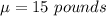
The standard deviation is:
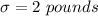
We are looking for a Z score for which it is met that:
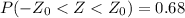
According to the empirical rule, for a standard normal distribution it is satisfied that 68% of the data is in a range of one standard deviation above the mean and one standard deviation below the mean. This means that:
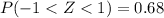
Then

Therefore