Answer: The graph of the basic parabola
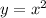 is shifted upward 5 units and shifted 2 units to the right.
is shifted upward 5 units and shifted 2 units to the right.
Explanation:
There are some transformations for a function f(x).
Some of this transformations are the following:
If
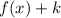 , then the function is shifted upward "k" units
, then the function is shifted upward "k" units
If
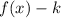 , then the function is shifted downward "k" units.
, then the function is shifted downward "k" units.
If
 , then the function is shifted to the left "k" units.
, then the function is shifted to the left "k" units.
If
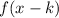 , then the function is shifted to the right "k" units.
, then the function is shifted to the right "k" units.
In this case we know that the equation
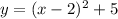 is obtained by transformating
is obtained by transformating
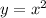 .
.
Therefore, based on the transformations mentioned before, we can describe how the equation
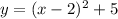 transforms the graph of the basic parabola
transforms the graph of the basic parabola
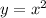 :
:
The graph of the basic parabola
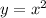 is shifted upward 5 units and shifted 2 units to the right.
is shifted upward 5 units and shifted 2 units to the right.