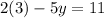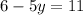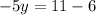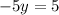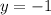Question

3x+2y=7,2x-5y=11. By elimination method, need all steps

Answer 1

`x=3,\ \ y=-1`

Explanation:

We have the following two equations:

`3x+2y=7`

`2x-5y=11`

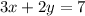
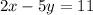
To solve the system by the elimination method multiply the first equation by
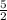`(5)/(2)` and add it to the second equation

By multiplying the first equation by
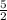`(5)/(2)` you get the following:

`(15)/(2)x+5y=(35)/(2)`

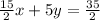
Now we add the two equations

`(15)/(2)x+5y=(35)/(2)`

`2x-5y=11`

---------------------------------------------------------

`(19)/(2)x=(57)/(2)\\\\19x=57\\\\x=(57)/(19)\\\\x=3`

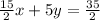
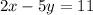
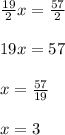
Now substitute the value of x in either equation and solve for y

`2(3)-5y=11`

`6-5y=11`

`-5y=11-6`

`-5y=5`

`y=-1`

Answer 2

x = 3 and y = -1

Explanation:

It is given that,

3x + 2y = 7 ----(1)

2x - 5y = 11 ---(2)

To find the solution of given equations

eq(1) * 2 ⇒

6x + 4y = 14 ----(3)

eq(2) * 3 ⇒

6x - 15y = 33 ----(4)

eq(3) - eq(4) ⇒

6x + 4y = 14 ----(3)

6x - 15y = 33 ----(4)

19y = 19

y = -1

Substitute the value of y in eq (1) we get,

3x + 2y = 7 ----(1)

3x + (2 *-1) = 7

3x = 7 + 2 = 9

x = 9/3 = 3

Therefore x = 3 and y = -1