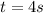Answer:
t = 4 s
Step-by-step explanation:
As we know that the particle A starts from Rest with constant acceleration
So the distance moved by the particle in given time "t"
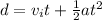
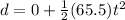
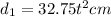
Now we know that B moves with constant speed so in the same time B will move to another distance
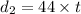
now we know that B is already 349 cm down the track
so if A and B will meet after time "t"
then in that case
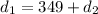
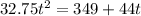
on solving above kinematics equation we have