Question

Please help me with this question. I’m stuck

Answer 1

(6,1)

Explanation:

To find the points of inflection, we need to find where the second derivative is equal to zero, or does not exist.

I will take the derivative using the chain rule.

`f(x) = 5\sqrt[3]{(x-6) } + 1 \\\\f(x) = 5(x-6)^{(1)/(3) }  + 1`

The first derivative:

`f'(x) = 5*(1)/(3) (x-6)^(-2/3) \\\\f'(x) = (5)/(3) (x-6)^(-2/3) \\`

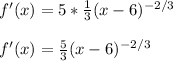
The second derivative:

`f'(x) = (5)/(3) (x-6)^(-2/3) \\\\f''(x) = (5)/(3)*-(2)/(3) (x-6)^(-5/3)\\\\ f''(x) = -(10)/(9) (x-6)^(-5/3)`

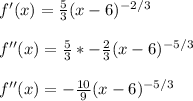
Now to find the inflection points we have to find where the second derivative is equal to zero, or do not exist.

`f''(x) = -(10)/(9) (x-6)^(-5/3)\\0= -(10)/(9) (x-6)^(-5/3)\\0= (x-6)^(-5/3)\\\\`

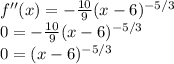
We can see that the second derivative does not exist when x=6, so there is an inflection point there.

We can solve the original equation to find the coordinate for x = 6.

f(x) = 5∛(x-6) + 1

f(6) = 5∛(6-6) + 1

f(6) = 1

So there is an inflection point at (6,1)