Question

Find the distance and midpoint of the line segment with endpoints (4,3) and (5,-2)

i know the answers i just need an explanation

Answer 1

The distance of the given points is
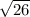`√(26)` units.

The midpoint of the given points is
`((9)/(2),(1)/(2))`.

Explanation:

The distance formula is:

`√((x_2-x_1)^2+(y_2-y_1)^2)`.

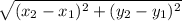So we need to find the x-difference and the y-difference.

After finding both differences we need to square each difference. (You should not get either square result to be negative. If you did, you did something wrong. You perhaps did not put your number in ( ).)

Then you add the squared results.

Final step, is to take the square root of your sum.

Let's do this.

x-difference: 5-4=1

y-difference: -2-3=-5

Square the x-difference: (1)^2=1

Square the y-difference: (-5)^2=25

Add the squared differences: 25+1=26

Square root the sum: √(26)

However if you don't like this, you just use the formula I wrote above:

`√((x_2-x_1)^2+(y_2-y_1)^2)`

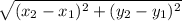
with
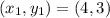`(x_1,y_1)=(4,3)` and
`(x_2,y_2)=(5,-2)`.

`√((5-4)^2+(-2-3)^2)`

`√((1)^2+(-5)^2)`

`√(1+25)`

`√(26)`

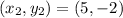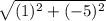
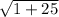
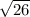
The distance of the given points is
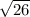`√(26)` units.

The midpoint formula given the endpoints
`(x_1,y_1)` and
`(x_2,y_2)` is:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`.

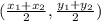You are just averaging the x's.

You are just averaging the y's.

The midpoint is (average of x , average of y).

To find average of the two numbers you just add the two numbers and then divide by 2.

So let's do that.

The sum of the x's: 4+5=9

The sum of the y's: 3+(-2)=1

The average of the x's: 9/2

The average of the y's: 1/2

The midpoint is (9/2 , 1/2).

Perhaps you would like to use the formula directly:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

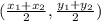
with
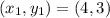`(x_1,y_1)=(4,3)` and
`(x_2,y_2)=(5,-2)`.

`((4+5)/(2),(3+(-2))/(2))`

`((9)/(2),(1)/(2))`

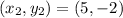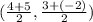
So (9/2 , 1/2) is the midpoint of the given points.

Answer 2

First let's find the midpoint:

The formula for midpoint is

(
`(x_(1)+x_(2))/(2)`,
`(y_(1)+y_(2))/(2)`)

Essentially what you are doing here is taking the mean of the two endpoints

In this case:

`x_(1) =4\\x_(2) =5\\y_(1) =3\\y_(2) =-2`

^^^Plug in these number into the formula given above...

(
`(4+5)/(2)`,
`(3+ (-2))/(2)`)

Your midpoint is:

(
`(9)/(2)`,
`(1)/(2)`)

OR

(4.5, 0.5)

Now let's find the distance:

The formula for distance between two points is:

`\sqrt{(x_(2) -x_(1))^(2) + (y_(2) -y_(1))^(2)}`

In this case:

`x_(2) =5\\x_(1) =4\\y_(2) =-2\\y_(1) =3`

^^^Plug these numbers into the formula for distance like so...

`\sqrt{(5-4)^(2) + (-2-3)^(2)}`

To solve this you must use the rules of PEMDAS (Parentheses, Exponent, Multiplication, Division, Addition, Subtraction)

First we have parentheses. Remember that when solving you must go from left to right

`\sqrt{(5-4)^(2) + (-2-3)^(2)}`

5 - 4 = 1

`\sqrt{(1)^(2) + (-2-3)^(2)}`

-2 - 3 = -5

`\sqrt{(1)^(2) + (-5)^(2)}`

Next solve the exponent. Again, you must do this from left to right

`\sqrt{(1)^(2) + (-5)^(2)}`

1² = 1

`\sqrt{1 + (-5)^(2)}`

(-5)² = 25

`√((1 + 25))`

Now for the addition

`√((1 + 25))`

1 + 25= 26

√26 <<<This can not be further simplified so this is your exact answer

Your approximate answer would be about 5.099 OR 5.10

***Remember that the above answers are in terms of units

Hope this helped!

~Just a girl in love with Shawn Mendes