Question

Table below shows probability distribution of siblings of students in a high school of 1500. What is expected value for the number of siblings of a randomly chosen student?

#of siblings- 0 1 2 3 4 5
probability- 0.20 0.65 0.08 0.04 0.02 0.01

a, 1.26 b, 2.5 c. 1.06 d.1.2

Answer 1

Answer: c, 1.06

Explanation:

Answer 2

Answer: Option C

`E =1.06\ siblings`

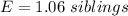
Explanation:

Let X be a discrete random variable that counts the number of siblings a randomly selected student has. Then the expected value of X is defined as:

`E =\sum_(i=0)^(i=n) X_iP(X_i)`

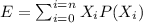
Where
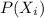`P(X_i)` is the probability that a randomly selected student has
`X_i` siblings

With
`i = \{0,1, 2, 3, 4, 5\}`

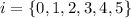
So in this case we know that

#of siblings 0 1 2 3 4 5

probability 0.20 0.65 0.08 0.04 0.02 0.01

Therefore:

`E =\sum_(i=0)^(i=5) X_iP(X_i)`

`E =0*(0.20)+1*(0.65)+2*(0.08)+3*(0.04)+4*(0.02)+5*(0.01)`

`E =1.06`

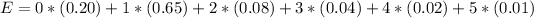
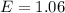
The answer is the option C.