Answer:
a)3
b)13/4
c)-4
d)5
NOTE: You might want to read the first section below the "Step-by-step explanation:" to see if I have interpreted your problems correctly.
Explanation:
a)

b)
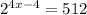
c)
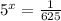
d)
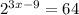
------------------------------------
a)
Let's writ ether the logarithmic form in equivalent exponential form:
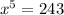
To solve this we need to take the fifth root of both sides:
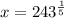

b)
We are going to write both sides so their bases are 2.
The left hand side is already base 2 so we are not doing anything to that side.
The 512 however can be written as 2^9.
So we have:
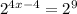
Since the bases are the same, the only thing we can do is set the exponents equal so those are the same as well.
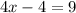
Add 4 on both sides:
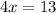
Divide both sides by 4:
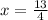
c)
We are going to write both sides so their bases are 5.
This does not effect left hand side since the base is already 5 on that side.
I know 5^4=625 so 5^(-4)=1/625.
So we have:
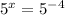
This implies
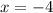 .
.
d)
We are going to write both sides so they have base 2.
Left hand side is done. Let's move on to the right. 64=2^6.
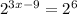 .
.
This implies:
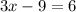
Add 9 on both sides:
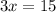
Divide both sides by 3:
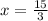
Simplify:
