Answer:
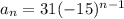
31, -465, 6975, -104,625, 1,569,375, -23,540,625
Explanation:
The formula for a geometric sequence is:
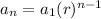
The formula for a geometric sequence is:
Where
r is the common ratio
 is the first term
is the first term
 is the nth term
is the nth term
In this case
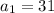
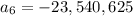
So:
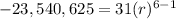
Now we solve for r
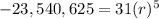
![-(23,540,625)/(31)=r^(5)\\\\r=\sqrt[5]{-(23,540,625)/(31)}\\\\r=-15](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sjti472igmkhk5ksntz7d8atp06vho0j5v.png)
Then the four geometric means are
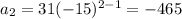
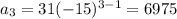
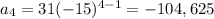
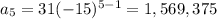
31, -465, 6975, -104,625, 1,569,375, -23,540,625