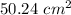For this case we have that the area of the shaded region is given by the subtraction of areas of both circles. That is to say:
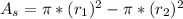
Where:
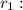 It is the radius of the major circle
It is the radius of the major circle
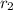 : It is the radius of the smaller circle
: It is the radius of the smaller circle
According to the data we have:
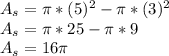
Taking

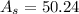
So, the area of the shaded region is
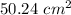
Answer: