Answer:
See explanation
Explanation:
A. The graph of the function
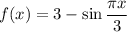 is shown in attached diagram.
is shown in attached diagram.
B. The period of the function
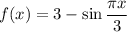 is
is

C. The values of
 are
are
![[-1,1],](https://img.qammunity.org/2020/formulas/mathematics/high-school/m2n7q8j21790khzc1qcqz467voipe5xoyp.png) so the maximum value of the function
so the maximum value of the function
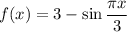 is
is

D. The smallest positive x for which f(x) is maximum is x=4.5 (black point on the graph).