Question

Help Please! <3

3. To combine the equations and solve for one of the variables, you need to eliminate the other variable. How can you change one equation so that one variable is eliminated when the two equations are added? Explain and write the new equation (The equations are 12x+6y=120 and 4x+y=30)

4. combine the two equations to eliminate one of the variables, and then solve for the other.


5. Solve for the other variable.


6. Prove that your solutions are correct by substituting the values back into the original equations and verifying the answers.

Answer 1

Explanation:

To eliminate the other variable x multiply the second equation by -3

Add both equations

12x +6y = 120

-12x -3y = -90

result of the addition: (-12x cancels 12x)

3y=30

y=10

4x +10 = 30

4x = 20

x=5

Plug into equations

4*5 +10 = 30 20 + 10 = 30

12*5 + 6*10 = 120 60 +60 = 120

Answer 2

For this case we have the following system of equations:

`12x + 6y = 120\\4x + y = 30`

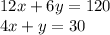
We must solve the system by the method of elimination. To do this we multiply the second equation by -3, then:

`12x + 6y = 120\\-12x-3y = -90`

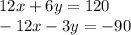
We add both equations:

`12x-12x + 6y-3y = 120-90\\3y = 30\\y = \frac {30} {3}\\y = 10`

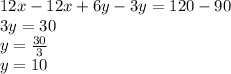
We find the value of "x":

`4x + y = 30\\4x + 10 = 30\\4x = 30-10\\4x = 20\\x = \frac {20} {4}\\x = 5`

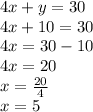
Thus, the solution of the system is:

`(x, y) :( 5,10)`

We verify:

`12 (5) +6 (10) = 120\\60 + 60 = 120\\120 = 120`

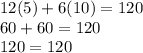
Is fulfilled!

`4 (5) + 10 = 30\\20 + 10 = 30\\30 = 30`

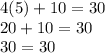
Is fulfilled!

Answer:

`(x, y) :( 5,10)`