Answer:
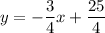 .
.
Explanation:
The equation of a circle of radius
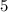 centered at
centered at
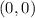 is:
is:
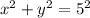 .
.
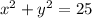 .
.
Differentiate implicitly with respect to
 to find the slope of tangents to this circle.
to find the slope of tangents to this circle.
![\displaystyle (d)/(dx)[x^(2) + y^(2)] = (d)/(dx)[25]](https://img.qammunity.org/2020/formulas/mathematics/high-school/yugdueoxjqc4ylie6gzvzbpqye05x2vq4k.png)
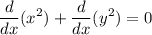 .
.
Apply the power rule and the chain rule. Treat
 as a function of
as a function of
 ,
,
 .
.
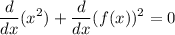 .
.
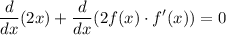 .
.
That is:
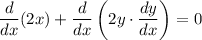 .
.
Solve this equation for
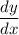 :
:
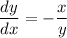 .
.
The slope of the tangent to this circle at point
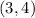 will thus equal
will thus equal
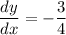 .
.
Apply the slope-point of a line in a cartesian plane:
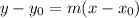 , where
, where
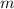 is the gradient of this line, and
is the gradient of this line, and
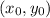 are the coordinates of a point on that line.
are the coordinates of a point on that line.
For the tangent line in this question:
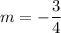 ,
,
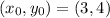 .
.
The equation of this tangent line will thus be:
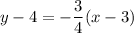 .
.
That simplifies to
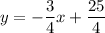 .
.