Question

A bottle filling process has a setting of 48 ounces which is exactly what consumers want when they buy the vegetable oil. A random sample of 36 bottles produced a sample mean of 48.15 ounces with a standard deviation of 0.3 ounces. Test the hypothesis at the 2% level of significance.

Answer 1

Answer with explanation:

Given : A bottle filling process has a setting of 48 ounces which is exactly what consumers want when they buy the vegetable oil.

Let
`\mu` represents the population mean .

Then, the set of hypothesis will be:-

`H_0: \mu=48`

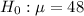
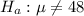`H_a:\mu\\eq48` , since the alternative hypothesis is two-tailed , so the hypothesis test is a two-tailed test.

We assume that this is normal distribution.

Sample size : n =36, which is a large sample (z<30) , so we use t-test.

Sample mean :
`\overliene{x}=48.15\text{ ounces}`

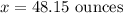
Standard deviation :
`\sigma=0.3\text{ ounces}`

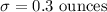
The test statistic for population mean for large sample is given by :-

`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`z=(48.15-48)/((0.3)/(√(36)))=3`

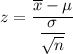
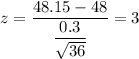
The p-value =
`2P(z>3)=0.0026998`

Since the p-value is less than the significance level of 0.02 , therefore we reject the null hypothesis and support the alternative hypothesis.

Thus we conclude that we do not have enough evidence to support the claim that a bottle filling process has a setting of 48 ounces which is exactly what consumers want when they buy the vegetable oil.