Question

John is organizing a local event. He expects the approximate attendance for the event to be modeled by the function a(t) = -16t2 + 48t + 64, where t is time in hours.

Assuming the event ends when there are no attendees, plot the domain to represent the duration of the event.
number line
< -5 -4 -3 -2 -1 0 1 2 3 4 5 >

Answer 1

0 ≤ t ≤ 4

Explanation:

Given function:

`a(t)=-16t^2+48t+64`

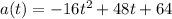
where:

• a(t) = number of attendees
• t = time (in hours)

The event starts when t = 0. This is the first endpoint of the domain.

If the event ends when there are no attendees, the other endpoint of the domain will be the greater value of t when a(t) = 0.

Set the function to zero and factor it:

`\implies -16t^2+48t+64=0`

`\implies -16(t^2-3t-4)=0`

`\implies t^2-3t-4=0`

`\implies t^2-4t+t-4=0`

`\implies t(t-4)+1(t-4)=0`

`\implies (t+1)(t-4)=0`

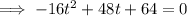
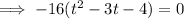
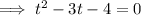
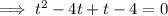
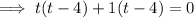
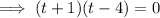
Apply the zero-product property:

`\implies t+1=0 \implies t=-1`

`\implies t-4=0 \implies t=4`

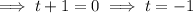
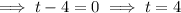
Therefore, the domain is 0 ≤ t ≤ 4.

When graphing inequalities on a number line:

• < or > : open dot
• ≤ or ≥ : closed dot

Therefore, to represent the found domain on the number line:

• Place a closed dot at t = 0.
• Place a closed dot at t = 4.
• Draw a line segment connecting both dots.