Question

A survey of 37 people was conducted to compare their self-reported height to their actual height. The difference between reported height and actual height was calculated. You're testing the claim that the mean difference is greater than 1.4. From the sample, the mean difference was 1.7, with a standard deviation of 0.58. Calculate the test statistic, rounded to two decimal places

Answer 1

(1.7-1.4)/(.58/
`√(37)`)

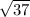Explanation:

To find the test statistic you need the sample mean, the mean you are testing for, the sample standard deviation and the sample size, all of which you have. then the formula is (sample mean - test mean)/(sample standard deviation/sqrt(sample size))

Also to make it easier I will list off what symbols are usually used for the different parts.

sample mean is
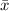`\bar{x}` (called x-bar) and population mean is μ (called mu) This is also the mean that is being tested for.

Sample standard deviation is s and population standard deviation is σ (called sigma)

Sizes are really similar, n is the sample size and N is the population size

So now you know the formula will look like
`\frac{\bar{x}-\mu}{(\sigma)/(√(n) ) }`

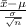
Now you just plug in. (1.7-1.4)/(.58/
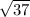`√(37)`). Solve and just round