Answer:
Time,
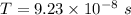
Step-by-step explanation:
It is given that,
Mass of proton,
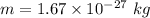
Charge on proton,
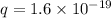
Magnetic field, B = 0.71 T
Time taken by proton to make one complete circular orbit is given by :


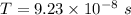
So, the time for the proton to make one complete circular orbit is
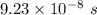 . Hence, this is the required solution.
. Hence, this is the required solution.