Question

New parents place a continuous stream of $5,000 per year into a college fund which has a continuously compounding interest rate of 0.8%. What will be the value of this continuous stream after 18 years? Round your answer to the nearest integer. Do not include a dollar sign or commas in your answer.

Answer 1

The value of this continuous stream after 18 years is going to be of 96435 dollars.

Step-by-step explanation:

We solve this problem calculating the stream for each year using the following formula:

`S_(t) = S_(t-1)*(1.008)+5000`

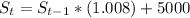
Where St is the value of the saving stream at year t, St-1 is the value of the saving stream from the previous year and t≥0.

This formula tells us that the current value of the saving stream at a given year is equal to the past savings plus the interests on those savings, plus the deposits on the saving account that are made that year (which will only bear interests at the end of the year).

Therefore when we compute the formula for each of the 18 years we obtain the following results:

Year 0 5.000,00

Year 1 5.040,00

Year 2 10.080,32

Year 3 15.160,96

Year 4 20.282,25

Year 5 25.444,51

Year 6 30.648,06

Year 7 35.893,25

Year 8 41.180,39

Year 9 46.509,84

Year 10 51.881,92

Year 11 57.296,97

Year 12 62.755,35

Year 13 68.257,39

Year 14 73.803,45

Year 15 79.393,88

Year 16 85.029,03

Year 17 90.709,26

Year 18 96.434,93

To conclude we can say that the value of this continuous stream after 18 years is going to be of 96,435 dollars.